Introduction to convolutional NN
The convolution operator 🟩-
Il prodotto di convoluzione è matematicamente molto contorto, anche se nella pratica è una cosa molto molto semplice. In pratica voglio calcolare il valore di un pixel in funzione di certi suoi vicini, moltiplicati per un filter che in pratica è una matrice di pesi, che definisce un pattern lineare a cui sarei interessato di cercare nell’immagine.
-
Slides ed esempi (molto più chiaril)
Vedi che per calcolare quell’8 sto facendo cose lineari con tutti pixel intorno ad essa.
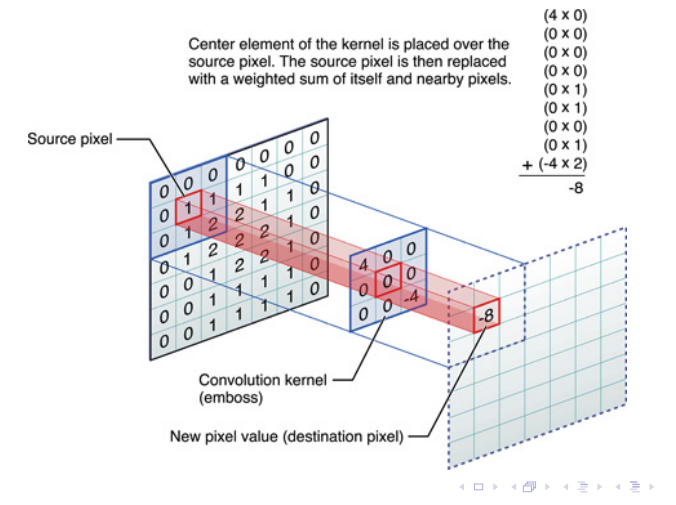
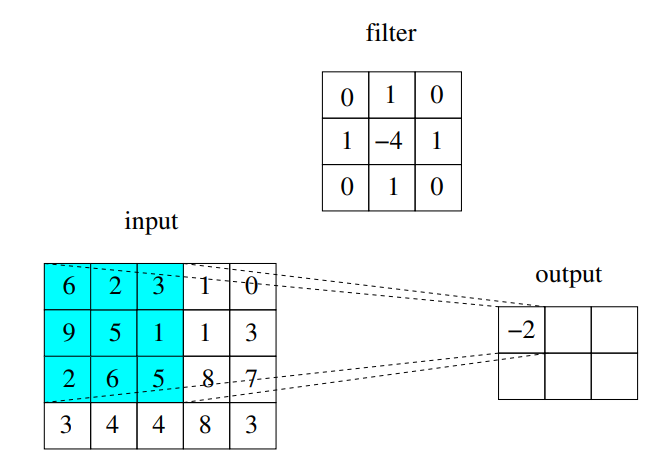
Questo operatore l’abbiamo già trattato in modo molto breve in Deblur di immagini.
Some properties and uses
Sappiamo tutti che le immagini non sono altro che arrai di valori in un certo intervallo, che rappresentano l’intensità dei colori, o solamente del bianco-grigio nel caso delle immagini grigio nere.
Queste intensità si potrebbero anche rappresentare come superfici 3d in cui la posizione del pixel identifica x e y, mentre l’intensità la z, abbiamo quindi proprio delle superfici!, delle montagne, valli fiumi etc. Le cose molto interessanti sono cambi di intensità improvvisi (con derivata molto alta) ossia i dirupi, le valli, questo cambio improvviso (il cambio di fase come dice Pedro di Master algorithm) è classico anche in nautura, è la parte con qualche informazione di interesse diciamo.
THE IDEA OF DERIVATIVE FOR CHANGES
- Slide finite approssimation of derivative

h = 1 perché siamo in campo discreto (è anche il minimo h che possiamo considerare in questo setting), quel filtro quindi ci è utile per capire se ci sono dei cambi improvvisi.
Questa idea ci permette di costruire il kernel per identificare le linee (visible contours of the image), orizzontali (cambi direzione e avresti verticale). it’s a feature map, of the image to some characteristic of the image. (ti dice se in questa zona è presente, non c’è , o c’è l’opposto del pattern che cercavi).
Some architectures
Deepwise separable convolution
Inception architecture 🟨
Andiamo a derfinire un modulo di inception (in cui va a fare in un certo senso scrambling, decomporre e recomporre dati, in che modo vanno ad estrarre delle features io non lo so!).
Comunque questa è l’architettura classica, andare ad utilizzare reti convoluzionali e poi operarle con reti deep (alla fine non molto deep) in modo da collegargli insieme.
- Esempio di inception module
!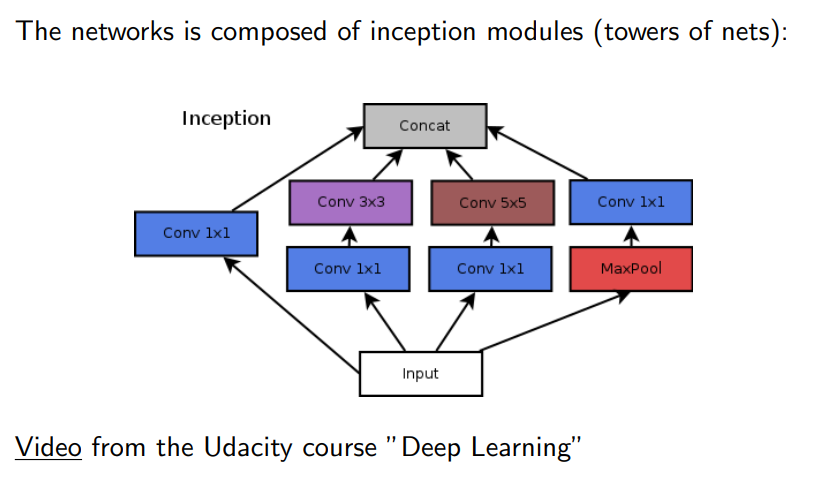
https://www.youtube.com/watch?v=VxhSouuSZDY&ab_channel=Udacity
Residual layers
Residual learning is the main concept of these networks, it’s when we have a direct link with the beginning! In pratica diamo la possibilità al neurone di scegliere di non modificare o invece sì l’input credo, provo a chiedermi se posso avere un valore migliore di quanto ho attualmente con qualche peso.
- Structure of residual layer
https://arxiv.org/pdf/1512.03385.pdf
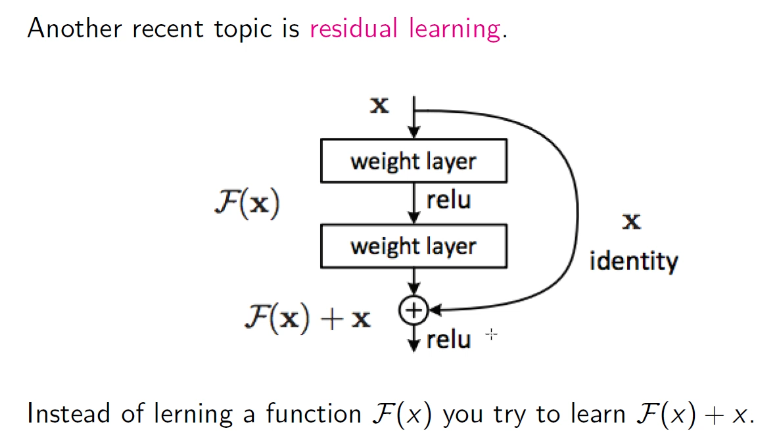
Usually these links help the network learn (lesser vanishing gradient.
Shattered Gradients
Most gradient descent methods assume to have a smooth gradient. This is not true anymore with very deep layers. Adding residual layers help ease this problem.
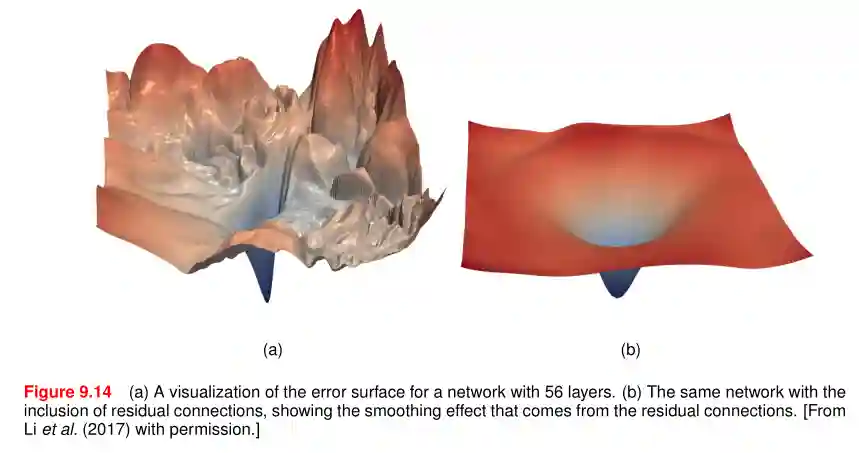
Smoother Error Surfaces
Introducing the residual layer helps in having smoother residual layers:
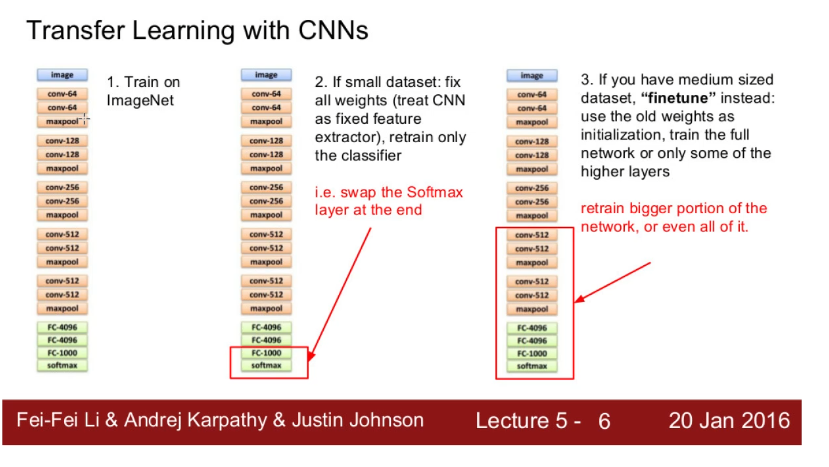
Transfer learning
-
Slide intuizione transfer learning
-
expected graph with performance with transfer learning
!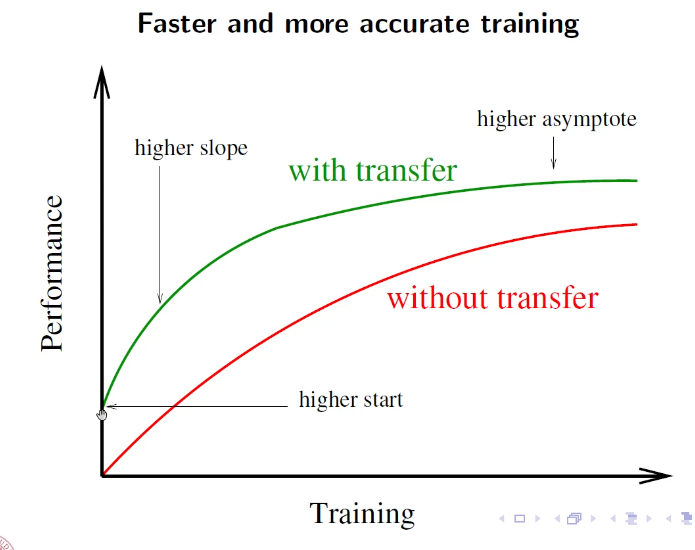
Comunque l’intuizione principale del transfer learning è l’idea che i primi layers facciano una sorta di estrazione di features più ad alto livello utili poi ai layers di deep NN. Se questa prima parte l’ho trainata su un corpus enorme, allora gli aspetti che è riuscito a generalizzare potrebbero essere utili anche per altro, e quindi utilizzo i pesi trovati in questa rete anche per altro, senza problemi.
Fine tune o finetuning è un pò rischioso, faccio un freeze di una parte del network più larga, potrei andare a overfittare e fare cose simili! Però ha più senso, ci aiuta a rendere l’intera architettura ancora più focussato in quello che vogliamo fare noi (in un certo senso forse dà via alcune generalizzazioni inutili nel nostro dominio)
Training of CNN
Backpropagation of CNNs 🟨++
We can unroll the input and output layers as a single linear trasformation of a deep network (with weights adjusted accordingly).
- Intuition of unrolling
!
But how do we unroll?? We can see everything as a matrix with $[input\_size \times output\_size]$ as you can see from the image in the toggle
- Slide convolution matrix of the weights
!
After we have modelled this matrix, we can learn using standard backpropagation we have talked about in Neural Networks.
Un problema per questo metodo è la matrice è sparsa se input è molto largo, e kernel piccolo, avrei un numero di zeri assurdo, quindi nemmeno molto efficiente da memorizzare in questo modo. (però possiamo computare in modo efficiente, ma questo non lo trattiamo).
Un altro aspetto di questa matrice è la ripetizione shiftata dei pesi, che sono gli stessi in ogni colonna della matrice, ma solamente shiftato. Questo cambia il modo di fare update dei pesi, si utilizza l’update con average pesato. fra le 4 computazioni delle 4 colonne in esempio.
Transposed convolutions
Dopo che ho fatto troppo downsampling con le CNN, vorrei tornare sù di dimensione (se per esempio un input è un’immagine. Trasposed convolutions ci permettono di tornare su di dimensione. (anche tecniche statistiche credo che funzionino).
- Slide transposed convolutions
! !
!
This technique is called transposed convolution because if we transpose the convolution matrix, we see that we are upscaling the input!. Però non ho capito in che modo funziona!
Dilated convolutions 🟩
- Slide intuizione di questo
!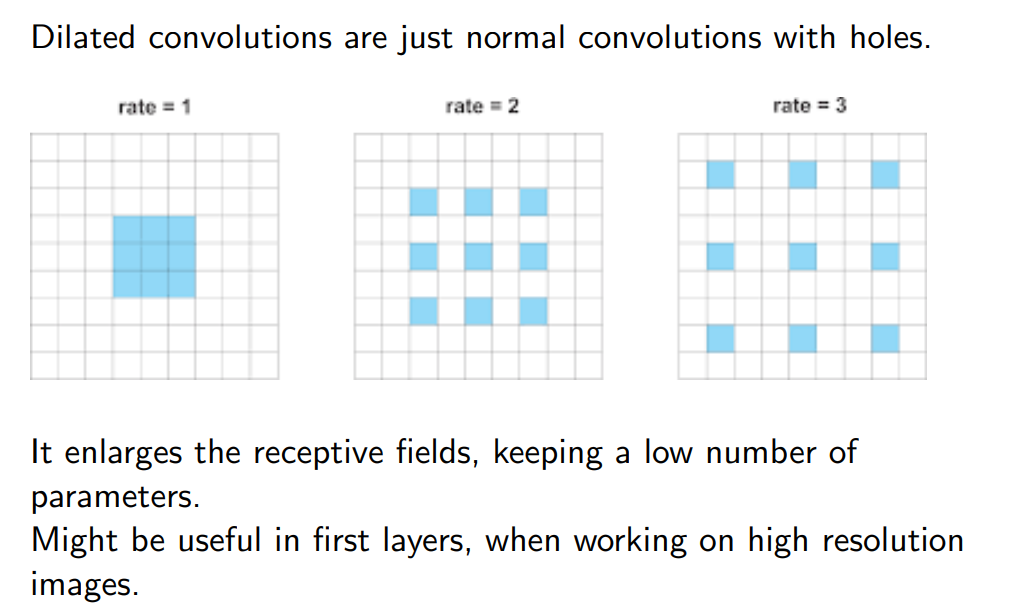
Facciamo una specie di padding interno sul kernel (non vado a contare certe cose, però riesco a ingrandire la receptive field del mio network.
Ha più senso fare sta cosa quando sto analizzando HIGH RESOLUTION IMAGE in cui il valore dei pixel cambia molto poco.
Una differenza con le Transposed convolutions 🟥 è il fatto che quelle sono fatte sull’input, questa la facciamo su come viene calcolato il kernel.
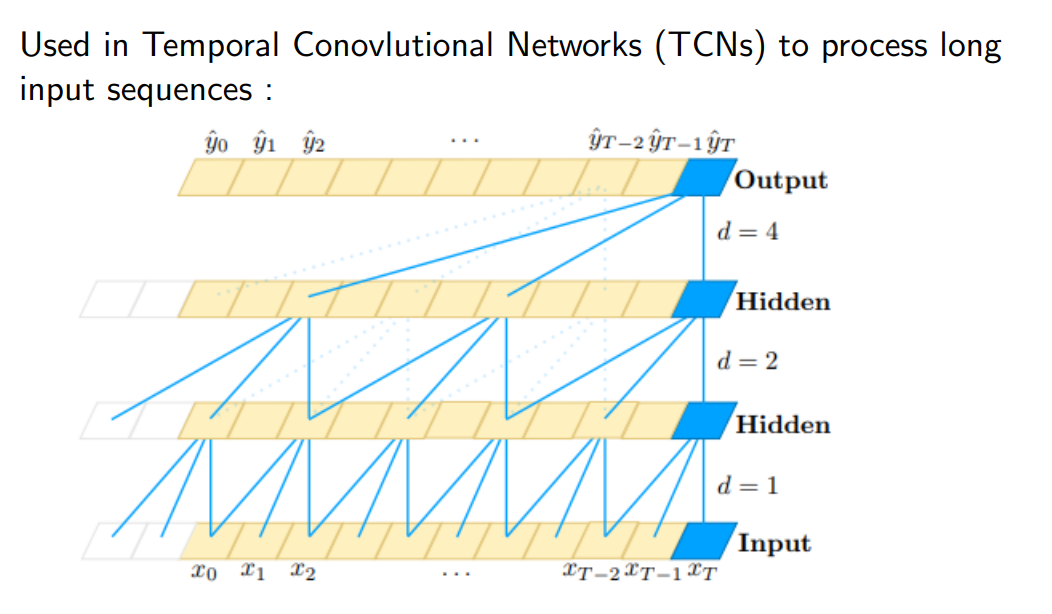
Sono molto utilizzate in temporal convolution networks, in cui provo a diluire volta per volta lo spazio all’interno del kernel, anche se non so ancora perché va
- Slide temporal convolution network
!
Normalization layers
Why normalization 🟥
- Slide 2 reasons
!
Why is normalization a good idea :D?
- So the quantitative values are comparable from each other (e.g. ages and income)
- We want the output of the layers to be comparable from each other, the middle outputs are inputs for other layers!
- We can better control the activation layers. (non vogliamo che faccia come output NaN 😟)
- Decoupling of the layers. (non dobbiamo andare ad imparare il range di input aspettato, dato che sarà sempre data di stesso tipo)
Batch Normalization 🟥
This is the most common form of normalization (ma l’idea è sempre la stessa, computare varianza e media, e poi sottrarre media e dividere per varianza). La cosa in più è che vengono aggiunte delle varianze e una media, per denormalizzare l’output, in modo che abbia la forma dei dati migliore possibile.
- Slide batch normalization
!

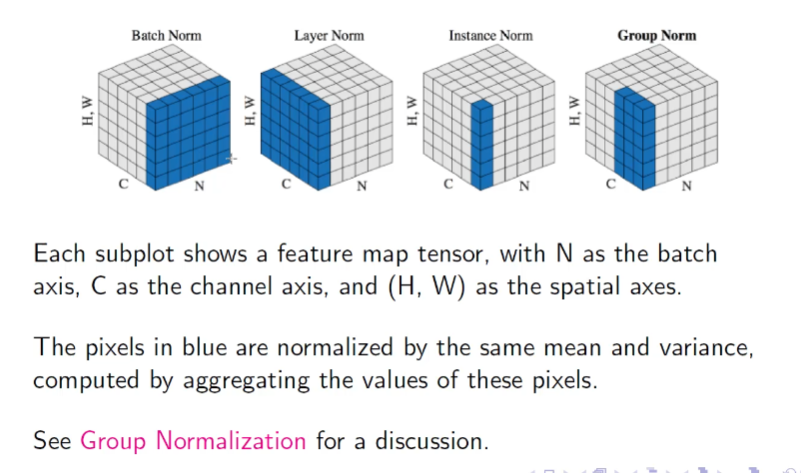
Other Normalization 🟥
Potremmo provare a normalizzare per canale
- Slide normalizations
!!