Ultima modifica: March 11, 2023 7:22 PM Primo Abbozzo: March 8, 2023 6:05 PM Studi Personali: No

Elementi di ripasso

Training of NN

How can we be sure that we can train well our function?

  1. Dataset quality (this cannot be changed in training time)
  2. Models and parameters of our model, we can describe it as $L(x, \theta)$, and we try to minimize this function.

Training approaches

  1. Random perturn weights, this is ispired by evolution, but it’s slow and not effective (and we can make things worse in many ways)
  2. Predict adjustments, usually we can analitically define what is the best way to minimize the loss, so we would like to follow that slope and go down!

When we try to learn with the second method we usually follow the direction of a derivative (this is also an idea of gradient descent that we discussed in Metodi di Discesa.

So if we have a step function, we can’t learn anything, this is not a good loss. This is the classic gradient descent, but the new thing is that we have optimizers, more on them later.

The standard Gradient descent uses the whole dataset to calculate the direction and module of descent. Usually this is quite expensive, why would we need to use all the data when a subset could be enough? And also, why can’t we use the last gradient to know where to go? There are the ideas for the next gradient descent methods.

Stochastic Gradient descent

  • faster
  • More noise

Sometimes when we try to escape from the noise, we can add some noise, like having a bigger step function, and we can escape a local minima if we get to.

Momentum

This is the other type of gradient descent, we add a momentum factor something like

$$ v_{t + 1} = \mu\nabla L(x) + \alpha v_t $$

The first term is the gradient (direction term) the second is the momentum term.

  • Slide on momentum

    image/universita/ex-notion/Training a NN/Untitled

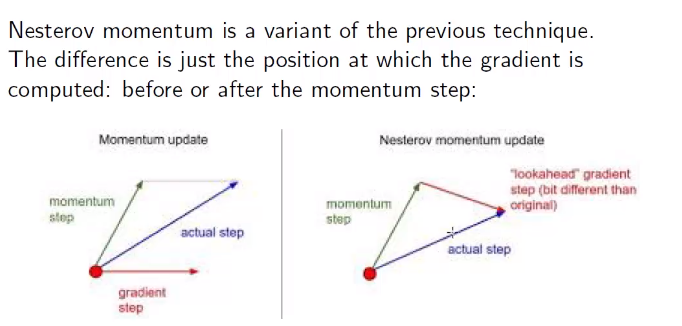
A different kind of momentum is nesterov momentum that just calculates the gradient from the next point after we applied the momentum, and not before, this should be a little better because we are just going from the gradient direction in an offsetted point, and not changing the gradient with some heuristic, (non mi sono affatto spiegato bene qui, non credo infatti di averlo capito bene sto momentum)

  • Slides nesterov

    image/universita/ex-notion/Training a NN/Untitled 1

Backpropagation

This is the gradient descent for neural networks.