Introduction
When a human first learns to program, the first concepts typically encountered are control flow, statements, loops, then functions, recursive calls, types, classes. If the person continues with this journey, an encounter with ideas like design patterns, architectural patterns, and software engineering practices are quite likely. In one way or another, these abstractions enable its general user to write portable software, without ever considering the microarchitecture that actually runs the compiled binaries beneath all the these abstractions. This is Computer Science’s fundamental magic: abstraction and implementation. However, sometimes abstractions are not so cleanly separated; they interact in complex manners that go beyond just exposing interfaces and implementing these interfaces, they actually influence each other in complex manners. As every complex system, they may display some strange feedback loops (Hofstadter 2007). But this is another story.
In this article, we will focus on practical ideas of implementation of fast software. This goal is not achievable by staying at some precise level of abstraction, but needs to consider the entire software stack, from compiler to cache systems to hardware optimizations of the specific microarchitecture that runs that software. We will focus specifically on single core optimizations of the software.
The next sections will be divided as follows: in we will discuss historical progress in writing fast software, including the introduction of super-scalar architectures BLAS/LAPACK (Angerson et al. 1990), FFTW (Frigo & Johnson 1998), vectorization. Then we will move on with a discussion of the main established techniques of optimization possibilities that new hardware is enabling. Finally, we end with clear examples and experiments on how such written software is evidently faster in running in modern architectures.
Most of this blog post has been a result of work following this paper (Huang et al. 2025) on practical optimization on specific CPU architectures of Clifford Kernels (generalization of imaginary kernels) useful for life sciences.
Motivation
Every computer scientist knows about compilers, cache mechanisms and some CPU architecture optimizations. However, few know about the optimizations that super-scalar architectures and later vectorization instructions have introduced in the last 30-40 years.
Super-scalar architectures have inherent form of parallelism; they execute more than one instruction per cycle using different parallel execution ports. Refer to the Intel i7 Skylake architecture for an example. Two things are important to notice here:
- Each architecture has usually more integer operation ports than floating point operations, which means flops are usually the bottleneck of the computation
- The upper limit of flops per cycle is easy to compute, and if you know the frequency of the core you can compute the flops per second. For example, in the figure we have two floating operation ports, each can execute one fused add-multiply operation per cycle, meaning four flops per cycle. If your processor runs at 4.8 Ghz, then your overall maximum theoretical upper bound is 19.2 Gigaflops per second. This value is usually never reachable due to data dependency patterns in the computation or memory transfer bottlenecks.

Example of Intel Skylake microarchitecture. We can observe the memory hierarchy, with latency and throughput counted as number of cycles needed to fetch the request, and number of doubles that can be stored or retrieved in a single instruction cycle. On the left we see the different execution ports. On the bottom left, we observe the instruction decoder and automatic out-of-order execution hardware engine (instruction pool). Slide from ASL ETH 2024 course. See here.
Compilers have limitations. Compilers are not able to optimize natively for these architectures. One requirement for compilers is the correctness of the compilation. Sadly, floating point operations do not possess associativity as one of their property. For example, consider the the following case:
#include <iostream>
int main() {
double a = 1e16;
double b = -1e16;
double c = 1.0;
double res1 = (a + b) + c;
double res2 = a + (b + c);
std::cout << "(a + b) + c = " << res1 << std::endl; // 0
std::cout << "a + (b + c) = " << res2 << std::endl; // 1
return 0;
}
Due to possible cases of overflow or underflow, floating-point operators adopt different approximation strategies that ultimately lead to different results. As we will see, this property is an important one.
Historical Results
Modern processor architectures commonly support the parallel execution of independent instructions through multiple execution ports, a design principle known as superscalar execution (Johnson 1989). However, effective exploitation of these hardware capabilities requires software that is explicitly written or optimized to take advantage of instruction-level parallelism (ILP), register renaming, and out-of-order execution.
Established linear algebra libraries such as LAPACK and BLAS have historically served as high-performance, portable foundations for numerical computations across platforms (Angerson et al. 1990). The ATLAS project further advanced this line of work by introducing automated empirical tuning techniques, enabling the generation of optimized kernels for different hardware configurations (Whaley & Dongarra 1998).
Despite their effectiveness, these libraries primarily target general matrix and vector operations, and may not yield optimal performance for more specialized computational workloads. This limitation has motivated the development of domain-specific software frameworks such as FFTW, which exploits the structure of the fast Fourier transform to achieve high efficiency on a wide range of platforms (Frigo & Johnson 2005, Frigo & Johnson 1998). Note that here it is the mathematical structure itself that enabled certain kinds of optimization in its relative hardware. It’s nice to observe such interplay between mathematical structures, software compositions and hardware architectures within this subfield of computer science.
Every relevant fast numerical software is somewhat inspired to these libraries. Modern PyTorch (Paszke et al. 2019), numpy library, use LAPACK and BLAS cores underneath to have a performance close to the theoretical upper limit.
In this post, we will mainly explore the optimizations that were introduced within the LAPACK libraries.
Optimization Strategies
In this section, we will explore established optimization techniques for single-core superscalar architectures. We will be exploring established techniques, nevertheless, they have proved to be valid after decades of architecture design. For example, some of the recent optimizations on GPU architectures have clear and recognizable ideas taken from these pioneering works (Dao et al. 2022). Here we mainly focus on matrix-matrix multiplication.
Instruction Level Parallelism
If a program is written in a certain manner where some data dependencies are present, we cannot leverage full throughput of the processor. However, if we rewrite the computation to include both cycle unrolling and different accumulators, we can exploit the underlying hardware optimizations and reach a far better performance. As you can see with the examples below, we can have a 2x performance improvement with just this little trick. Simple but effective technique.
Mini Matrix-Matrix Multiplication

Examples of forms of computation. (a) we see classical matrix-matrix multiplication: for each row and column we have a single value in C. Potentially for big matrices every element in B needs to be loaded again and again, creating memory bottlenecks. (b) blocked matrix matrix multiplication, where we better exploit cache locality to operate on the matrices. (c) Outer product for better ILP, only applied to very small matrices in the inner loop.
To understand this section, you will need a clear bachelor-level understanding of how CPU cache systems work. Another personally surprising reason why other more efficient algorithms for MMM multiplication are not actually faster than a good implementation of the naïve algorithm is due to cache-friendlyness limitations as we will see.
When optimizing matrix-matrix multiplication (MMM) for single-core execution, a major bottleneck emerges not in arithmetic but in data movement, particularly cache misses. To understand and mitigate this, we analyze the cache behavior of naïve vs. blocked matrix multiplication. This section will guide you through that analysis and show how a seemingly simple refactoring, blocking, dramatically improves performance. Blocking is the idea of dividing the whole matrix-matrix multiplication in many smaller cache-friendly block-level matrix multiplications.
Now, we consider the standard triple-loop implementation of matrix multiplication. We make the following assumptions:
- all matrices are stored in row-major order
- All the matrices are square matrices of size $n \times n$:
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
for (int k = 0; k < n; ++k)
C[i][j] += A[i][k] * B[k][j];
In contrast, a blocked-matrix multiplication of block size $b < n$ and $b$ divides $n$ is:
for (int ii = 0; ii < n; ii += b)
for (int jj = 0; jj < n; jj += b)
for (int kk = 0; kk < n; kk += b)
for (int i = ii; i < ii + b; ++i)
for (int j = jj; j < jj + b; ++j)
for (int k = kk; k < kk + b; ++k)
C[i][j] += A[i][k] * B[k][j];
As we will observe this version better exploits a cache’s spatial locality. %% we try to put some images to explain why this is better, needs one image per section I think. %%
Cache Miss Analysis: Naive vs Blocked
In the following analysis, we will only consider cache size, but in real systems (Angerson et al. 1990 ), also TLB page size and other cache configurations like associativity, size, and line size, are kept into consideration.
In the naïve implementation, we repeatedly access entire rows of $A$, columns of $B$, and write single entries of $C$. Due to row-major layout, accessing columns of B is especially harmful because it causes non-contiguous memory accesses. We we assume a single row of $B$ is big enough that it doesn’t fit into the cache, this means we will load a whole line block for every access in $B$.
Each access to a new element in a row or column causes a cache miss unless it’s already cached. We assume here a common cache block of 8 doubles and cache size of $\gamma \ll n$, we estimate:
- Accessing a row of $A$ causes $n / 8$ misses.
- Accessing a column of $B$ (non-contiguous) causes $n^{2}$ misses.
- So each entry computation causes about $9n / 8$ misses.
- Total number of entries computed: $n^{2}$.
- Total cache misses: $9n^{3} / 8$.
Now compare this with blocked matrix multiplication, where the matrix is split into sub-blocks of size $b \times b$. If we pick $b$ such that the entire sub-multiplication of blocks of size $b\times b$ fits in the cache, we can observe far fewer losses. Let $\gamma$ be the cache size as before. We require:
$$ \begin{align*} 3b^{2} &\leq \gamma & \text{ One block each of A, B, C} \\ \implies &b = \sqrt{ \frac{\gamma}{3} } \end{align*} $$$$ (n / b)^{2} \cdot nb / 4 = n^{3} / 4b $$We can observe the number of cache misses is far lower compared to the previous case. The bigger the $b$ is better here.
Micro Matrix-Matrix Multiplication
After applying blocking to make our computation cache-friendly, we can push optimization even further by going to the register level. The idea is to trade faster and more parallelized register operations with a little higher number of operations.
Analysis of Loop Reordering.
In a standard i-j-k ordering with indices set as #Mini Matrix-Matrix Multiplication, for each fixed (i,j) pair, we’re essentially computing a dot product: just 2n operations with $n$ data dependent additions. This has a lower instruction-level parallelism and lower number of operations compared to the next version:
If we flip to k-i-j ordering, we can observe the following. For each fixed $k$ we’re now performing a rank-1 update: taking an entire column from matrix A and an entire row from matrix B, and doing an outer product that updates the entire C block. This gives us $2n^{2}$ operations that are almost completely independent, correctly leveraging both instruction level parallelism and faster access with Cache blocks.
What makes micro-MMMs so effective is that they exploit a balance between cache locality and instruction-level parallelism. The blocks are small enough that data stays in registers, but the computation pattern generates enough independent operations to keep all execution ports busy.
Libraries like ATLAS, OpenBLAS, and Intel MKL all use variations of this technique. They’ll typically have hand-optimized micro-kernels for different tile sizes (2×2, 4×4, 6×8, etc.) depending on the target architecture’s register file size and execution port configuration.
Other Operations
Up until now, we covered some classical but general techniques for modern CPU architectures in the matrix-matrix setting. Sometimes we can take other considerations into account and further optimize by taking these into account.
Strength Reduction. See the wikipedia page. Here we will just give the general idea. If we look at Agner Fog’s tables, we observe that most of the division operations are slow in terms of cycles with respect to multiplication. This motivates substituting some complex operations with equivalent or similar precision operations. With a similar idea, sometimes it is useful to cache or pre-compute intermediary results. Most of the times, it is difficult to identify when you can optimize with this tricks. Lots of the optimizations come from experience, or just a lot of trial and error.
Vectorization Operations
Once we’ve optimized for instruction-level parallelism and cache locality, the next powerful lever is data-level parallelism, also known as vectorization.
Vectorization is the process of transforming scalar operations (working on one data element at a time) into SIMD (Single Instruction, Multiple Data) instructions that operate on multiple data elements in parallel. On x86 architectures, these are realized via AVX (Advanced Vector Extensions), SSE, or the newer AVX-512 instruction sets.
A simple example: instead of computing
for (int i = 0; i < 4; ++i)
C[i] = A[i] + B[i];
the compiler or programmer can generate a single SIMD instruction that does all four additions at once—assuming A, B, and C are properly aligned and stored contiguously.
This is possible thanks to SIMD registers implemented in every modern architecture:
- AVX: 256-bit registers → 4 doubles or 8 floats
- AVX-512: 512-bit registers → 8 doubles or 16 floats
Using these, you can execute operations like fused multiply-add (FMA) on multiple elements at once, within a single cycle. This gives a multiplicative factor to throughput, but only if your data layout and dependencies allow it.

(a) a visual representation of AVX-style SIMD operations. Each SIMD register packs multiple doubles, and SIMD instructions operate element-wise on all packed values, executed as a single operation. (b) normal operations in for loop (4 times more operations)
Hand-Vectorization: Intrinsics and Assembly
In many occasions, auto-vectorization, is not able to rewrite the computation in a manner that is compatible to vectorization: examples like loading from different parts of the memory, shuffling operations are beyond current compiler abilities. For this reason, if we already know the target architecture of our code, we can have some benefit by writing intrinsics: these are C-like wrappers for low-level SIMD instructions. For example, using AVX intrinsics:
#include <immintrin.h>
__m256d a = _mm256_load_pd(&A[i]);
__m256d b = _mm256_load_pd(&B[i]);
__m256d c = _mm256_add_pd(a, b);
_mm256_store_pd(&C[i], c);
You now manually pack, compute, and unpack using 256-bit wide registers. This has the highest performance gain in terms of throughput when the computation is compute bound, but it suffers from portability since this code runs only on machines with AVX intrinsics (mostly intel machines). In many cases, when data movement is the bottleneck, having these instructions would not even have any significant gain.
The next and final section will show a real example of these techniques applied in practice.
Experiments
We proceed with showing concrete results of the above optimization methods for two cases: (1) simple sum with Instruction-Level Parallelism, and (2) common matrix-matrix multiplication operations.
We run the experiments on an Intel Core i7-1280P, based on the Alder Lake architecture, with a base frequency of:
- Performance cores: 1.8 GHz
- Efficient cores: 1.3 GHz
This architecture features two ports for floating-point operations, and typical multiplication and addition instructions take four clock cycles.
- L1 Cache (Data): 48 KB (Golden Cove)
- L2 Cache: 1.25 MB (Golden Cove)
- L3 Cache: 24 MB total (3 MB × 8 Gracemont cores)
Experiment code is released in the github page.
We compile our code using GCC 13.3.0 with the following flags
-O3 -march=native -ffast-math -fno-tree-vectorize -mfma -mavx2We deactivate turboboost on the computer by setting the flag in/sys/devices/system/cpu/intel_pstate/no_turboto 1 in the Linux System.
The results are an average over 100 runs per function assuming cold cache, i.e. the values have not been loaded before into the CPU caches.
Results
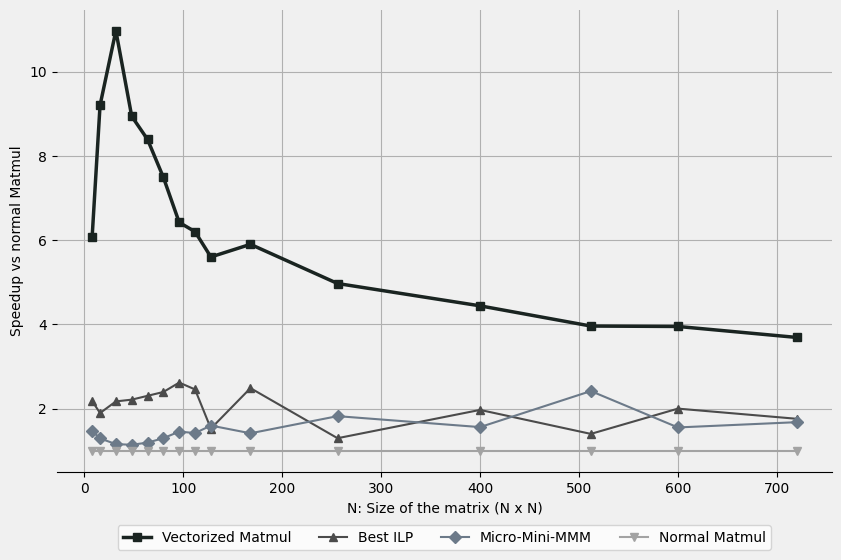
We report speedups compared to the naïve baseline version. We observe a simple vectorization is able to provide the greatest speedup. Even simple ILP changes are enough to double the original performance. If we analyze the flops/cycle, we can observe the current version is far from optimal performance, but it is enough to showcase how simple methods can greatly enhance performance with these computations.
Instruction-Level Parallelism. We observe that if we just unroll the loop, it is difficult to get any important speedup. Only if we add accumulators, we get more of the benefits present due to the intrinsic hardware parallelization primitives.
Micro and Mini Matrix-Matrix-Multiplication. Remember, these techniques are useful to exploit better cache friendliness for the architecture, they become important when the matrix size grows, and whole matrices don’t fit into the caches anymore. If they do fit, these techniques lose their winning point. With the current architecture and cache size above, the working set (set of floating point numbers that are often re-used, sharing time-locality) of the matrix matrix multiplication is mostly the entire $B$ matrix, one row of $A$ and a cache line for $C$ for the standard matrix matrix multiplication: we approximate the needed size to be a single matrix, then we have that with $N > \sqrt{ \frac{48000}{4} } \approx 109$ the matrix does not fit into the L1 cache anymore (we divided by 4 since each floating point is 4 bytes) and starting from $N > 559$ it does not fit into the L2 cache anymore.
On the slowdowns. We further notice that in the cold cache scenario, the small values for matrix size lose some of its time. Another slowdown that we observe and that we have not covered in this post is due to TLB cache misses for virtual paging, which is particularly relevant especially for power of two. You can observe that $512 \cdot 4$ is exactly half of page size in common Linux systems.
Conclusion
In this post, we covered the most common and established optimization techniques for single core CPU optimization. In particular, we covered important concepts like instruction-level parallelism, cache analysis and examples of cache friendly reformulation of the computations and showed how they can improve the performance of software in practice, delivering real speedups. We briefly touched over existing optimized software, like LAPACK/BLAS (Angerson et al. 1990) and frameworks like PyTorch that use these libraries underneath. Out in the wild, there are far more optimization techniques designed for some specific kinds of computation (Frigo & Johnson 1998, Dao et al. 2022), sparse computations, or GPU operations.
Citation
If you want to reference this work cite it as:
Huang, Xuanqiang Angelo “Optimizing Single-Core CPU software.” X. Angelo Huang’s Blog (Oct 2025). https://flecart.github.io/posts/2025-10-21-optimizing-single-core-cpu-software/
Or:
@article{huang2025optimizingsingle,
title = "Optimizing Single-Core CPU software.",
author = "Huang, Xuanqiang Angelo",
journal = "flecart.github.io",
year = "2025",
month = "Oct",
url = "flecart.github.io/posts/2025-10-21-optimizing-single-core-cpu-software/"
}
And take a look at the related paper in Huang et al. 2025.
References
[1] Angerson et al. “LAPACK: A Portable Linear Algebra Library for High-Performance Computers” Supercomputing '90:Proceedings of the 1990 ACM/IEEE Conference on Supercomputing 1990
[2] Frigo & Johnson “FFTW: An Adaptive Software Architecture for the FFT” IEEE 1998
[3] Hofstadter “I Am a Strange Loop” Basic Books 2007
[4] Huang et al. “Single-Core Superscalar Optimization of Clifford Neural Layers” arXiv preprint arXiv:2510.03290 2025
[5] Whaley & Dongarra “Automatically Tuned Linear Algebra Software” IEEE 1998
[6] Frigo & Johnson “The Design and Implementation of FFTW3” Proceedings of the IEEE Vol. 93(2), pp. 216--231 2005
[7] Dao et al. “FLASHATTENTION: Fast and Memory-Efficient Exact Attention with IO-awareness” Curran Associates Inc. 2022
[8] Johnson “Super-Scalar Processor Design” 1989
[9] Paszke et al. “PyTorch: An Imperative Style, High-Performance Deep Learning Library” None 2019