Impostazione del problema
Supponiamo di stare giocando a n slot machine contemporaneamente. Queste macchine hanno internamente un valore di reward che non conosciamo. Ad ogni step possiamo scegliere una singola macchina e andare a tirare la sua leva. Riceviamo il valore del reward nascosto con un pò di rumore. Vogliamo capire nel lungo quale sia la strategia che possa dare migliore reward medio possibile.
Questo è un semplice problema, ma lo possiamo considerare un fulcro molto importante per poter comprendere meglio reinforcement learning.
The mathematical model
Il numero di possibilità da esplorare è molto più ampio rispetto a quanto possiamo esplorare. Quindi, da quanto abbiamo ottenuto, vogliamo cercare di estrapolare possibili reward futuri. Supponiamo quindi $f \in \mathcal{F}$ che è lo spazio delle funzioni possibili non conosciute, abbiamo che $f : D \to \mathbb{R}$. Quello che osserviamo noi è $y = f + \varepsilon$ dove $\varepsilon$ è un rumore gaussiano. L’obiettivo è massimizzare il reward sul tempo, assumendo che $R_{t}$ sia il reward al tempo $t$. Per farlo abbiamo bisogno di trovare una policy. Teniamo sempre le definizioni di action value, optimal value.
Def: Regret, action value and optimal value
Action value $q(a) = E[R_t | A_t = a]$
Optimal value $V = \max_a q(a)$
Regret Ossia rappresenta quanto potremmo fare meglio., anche chiamato instantaneous regret.
$$ \Delta_{a} = v_{*} - q(a) $$Total regret
$$ L_{t} = \sum_{n=1}^{t} \Delta_{A_{n}} $$Ossia tutti i regrets per l’azione del tempo, e possiamo anche considerare la media per questo. Vorremmo sia esplorare, che cercare di sfruttare la soluzione migliore trovata finora.
Soluzioni classiche
I metodi presentati sono
- Optimistic initial value
- Mean-reward
- UCB choice Presi da (Sutton & Barto 2018).
GP-UCB
The idea
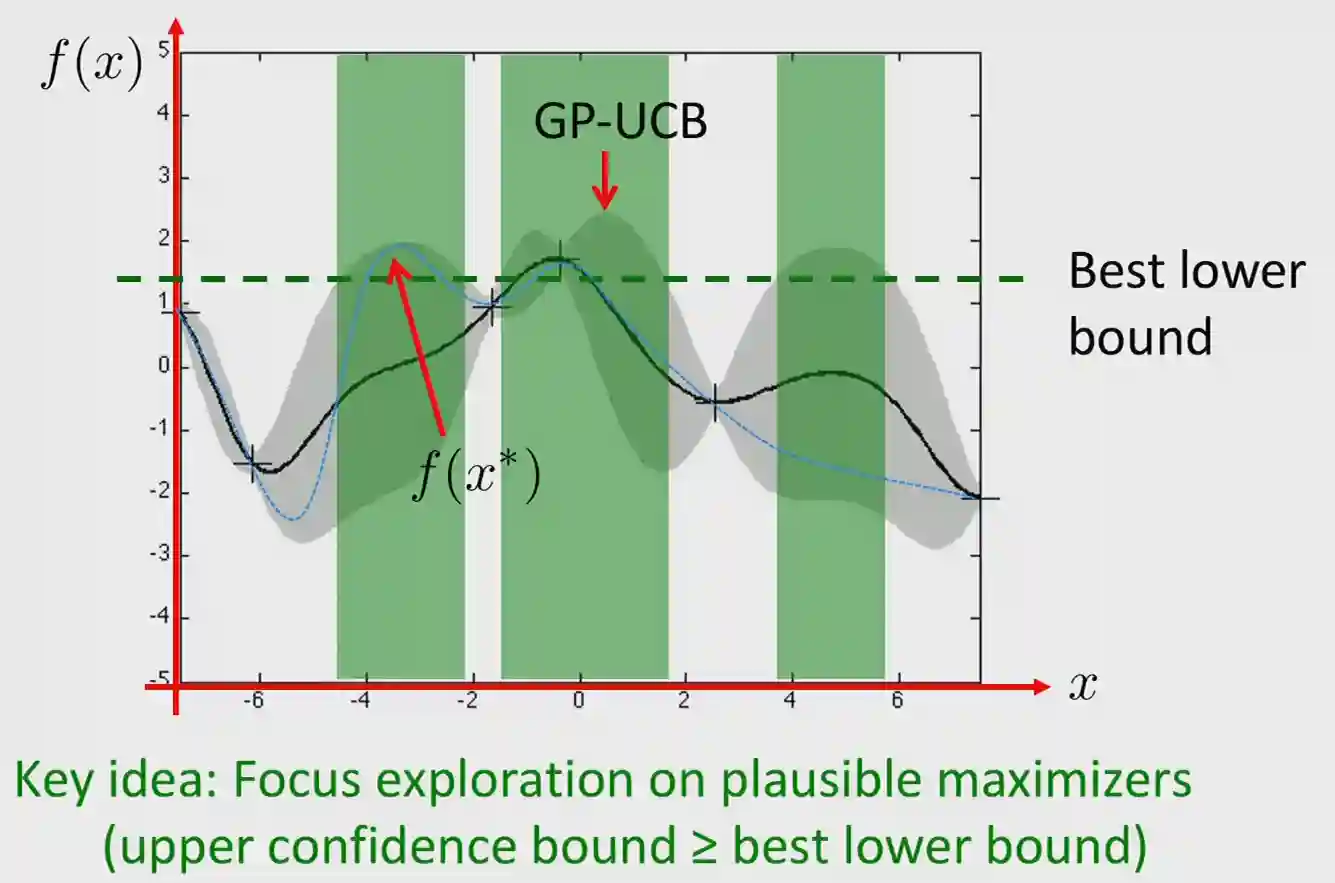 Image taken from slides of the PAI course ETH 2024.
Image taken from slides of the PAI course ETH 2024.
Optimism in the face of uncertanty
We just want to pick the point that maximizes our upper confidence bound in the posterior of the Gaussian Processes. The green region are the possible regions that we would like to sample from, as their upper confidence is higher than our lower bound. This idea is recurring in this setting.
This is formalized as
$$ x_{t} = \arg\max_{x \in D} \mu_{t - 1}(x) + \beta_{t - 1} \sigma_{t - 1}(x) $$Where $\mu_{t - 1}(x)$ is the mean of the GP at the point $x$ and $\sigma_{t - 1}(x)$ is the standard deviation. $\beta_{t - 1}$ is a parameter that we can tune to have more or less exploration. This should select the point that maximizes the upper confidence bound in the GP.
Convergence Bound on GP-UCP
The convergence bound on the GP-UCB is
$$ \frac{1}{T} \sum_{t = 1}^{T} (\mu_{*} - \mu_{t}) = \mathcal{O}\left( \sqrt{\frac{\max I(f; y_{s})}{T}} \right) $$
The maximum information gain determines the regret, often indicated as $\gamma_{T}$. This sets the rate at which I can get information.
I have no idea why this is true.
These are the bounds for different kernels in the GP

Mean-Reward
Vogliamo cercare di capire quale sia il valore nascosto all’interno di questi cosi. Possiamo supporre di avere un valore di default per ogni slot machine. Poi la strategia seguirà questo pseudo codice
def make_choice(
extimate_r, # /*array of extimates*/,
epsilon # /* exploration-exploitation balance */
):
x = random_sample from 0 to 1 // uniform distribution
if (x <= epsilon): // explore
idx = random choice x from all r
else:
idx = argmax(extimate_r);
return idx;
Dopo aver fatto la scelta, cercheremo di aggiornare il valore del reward seguendo proprio la media, quindi
$R_k = (r_k + \dfrac{1}{(k -1)} R_{k - 1}) / k$, con rk il reward attuale e quella il nuovo robo, anche se solitamente questa formula la si troverà scritta in questo modo, perché più carina
$$ R_k = R_{k - 1} + \dfrac{1}{k}( r_k - R_{k - 1}) $$Questo è il classico reinforcement learning per sta roba. UCB cambia solo nella selezione dell’indice da esplorare, che lo fa con la formula dipendente dal numero di esplorazioni fatte su questo, sugli altri nodi e simili.
mentre il optimistic initial value è molto particolare, si assegna un valore molto ottimistico, poi 0 al valore epsilon per l’esplorazione, poi piano piano tutte le mosse scendono di valore, fin quando non diventano realistiche.
Greedy solutions
Estimate of the average
$$ Q_t(a) = \frac{\sum_{n=1}^t I(A_n = a) R_n}{\sum_{n=1}^t I(A_n = a)} $$Questo si può fare anche in modo incrementale:
$$ Q_{t}(A_{t})) = Q_{t- 1} (A_{t} + \alpha_{t}(R_{t} - Q_{t - 1} (A_{t}))) $$Dove l’ultima parte è un errore. e $\alpha_{t} = \frac{1}{N_{t}(A_{t})}$
Greedy based
See Tabular Reinforcement Learning
Gradient Based
Policy search
Action preferences proviamo a stimare
$$ \pi(a) = \frac{e^{H_{t}(a)}}{\sum_{b} e^{H_{t}(b)}} $$Utile per avere distribuzioni di probabilità. Vogliamo trovare action preferences per policies migliori. Questo ci permette di utilizzare gradient ascent per migliorare il $\pi$.
Abbiamo quindi
$$ \theta_{t + 1} = \theta_{t} + \alpha \nabla_{\theta}\mathbf{E}[R_{t} | \pi_{\theta_{t}}] $$E ci permette di fare gradient ascent. Abbiamo un problema di come fare sample.
Usiamo (Williams 1992). Chiamato anche Reinforce. Da quello e da questo punto della lezione deriviamo
$$ \nabla_{\theta}\mathbf{E}[R_{t}|\theta] = \nabla_{\theta}\mathbf{E}[R_{t}\nabla_{\theta}\log \pi_{\theta}(A_{t})] $$E si può fare classico gradient ascent con la parte dentro all’argomento.
Proviamo avere questo algoritmo per action preferences
$$ H_{t+1}(a) = H_{t}(a) + \alpha R_{T} \frac{\delta \log\pi_{t}(A_{t})}{\delta H_{t}(a)} = H_{t}(a) + \alpha R_{t} (\mathbb{1}(a = A_{t}) - \pi_{t}(a)) $$È un esercizio provare a derivare questo cosa.
The upper confidence bound
L’idea è
- Selezionare se l’azione è big reward
- Selezionare se l’azione non è ancora stata esplorata abbastanza
Quindi come per il precedente, che vogliamo esplorare ancora, con la differenza che però vorremmo diminuire la possibilità nel caso fosse esplorata abbastanza
L’algoritmo sembra poi molto simile ai greedy, solo che abbiamo una funzione di UCB in più. Logarithmic regret as upperbound! (Auer et al 2002 questa roba).
Hoeffding’s Inequality
How wrong is our extimate? Consider $X_{1}, X_{2}, \dots, X_{n}$ variabili randomiche in 0, 1 con una certa media. rappresenteranno il nostro reward, e assumiamo che $\bar{X}$ ma media fino a $n$, in un certo senso simile ai bounds che stavamo studiando in Central Limit Theorem and Law of Large Numbers. La differenza con Markov e Chebicheff è che qui scende in modo esponenziale.
$$ p\left(\overline{X}_{n}+u\leq\mu\right)\leq\,e^{-2n u^{2}} $$Questo è un caso particolare in cui $b = 1, a = 0$ e funziona.
Possiamo utilizzare questo teorema con $R_{t}$, infatti possiamo vedere che
$$ p(Q_{t}(a) + U_{t}(a) \leq q(a)) \leq \exp(-2N_{t}(a) U_{t}(a)^{2}) $$E vale per qualche motivo strano anche con la -
$$ p(Q_{t}(a) - U_{t}(a) \geq q(a)) \leq \exp(-2N_{t}(a) U_{t}(a)^{2}) $$Questo teorema giustifica perché vogliamo scegliere il bound come questo valore:
$$ U_{t}(a) = \sqrt{ \frac{-\log p}{ 2N_{t}(a)} } $$$p$ possiamo stimarlo come il numero di volte che prendiamo quel valore nella nostra ricerca, quindi $p = \frac{1}{t}$ . Questo è la spiegazione teorica del perché il branch di esplorazione che abbiamo fatto durante il primo anno per il progetto di algoritmi funziona.
Lai and Robbins on Regret growth
$$ \lim_{ t \to \infty } L_{t} \geq \log t \sum_{a| \Delta_{a}} \frac{\Delta_{a}}{KL(\mathcal{R}_{a} \mid\mid \mathcal{R}_{a^{*}})} $$Ossia il total regret è bounded sotto almeno logaritmica-mente! Quindi se riesco a boundarlo sopra ho la cosa tight.
Derivation of the algorithm
Consideriamo $L_{t}$ che è il total regret numero di volte che selezioniamo l’azione, per il regret atteso.
$$ L_{t} = \sum_{a} N_{t}(a) \Delta_{a} $$E vorremmo che questa cosa sia il più basso possibile affinché possa risultare utile. Supponiamo che sia bounded. Ossia che per ogni $a = a^{*}$ valga $N_{t}(a) \Delta_{a} \leq x_{a} \log t$ .
Vorremmo trovare con una versione di UCB, che ci serve per selezionare l’azione.
Ora prendiamo $m \leq t$ allora dovrebbe valere che $N_{m}(a) \Delta_{a} \leq x_{a} \log m \leq x_{a} \log t$
Probability Matching and Thompson sampling
Vogliamo scegliere l’azione che possa sembrare la migliore secondo la nostra credenza:
$$ \pi_{t}(a) = p\left(q(a) = \max_{a'}q(a') | \mathcal{H}_{t - 1}\right) $$Per calcolare questo si può utilizzare Thompson sampling.
- Sample $Q_{t}(a) ~~~ p_{t}q(a)$
- Seleziona l’azione che massimizza $Q_{t}(a)$ per ogni $a$ all’interno di $\mathcal{A}$. Questo si avvicina al limite teorico ottimo, quindi nice. Ma il problema è che non sono scalabili questi algoritmi.
TODO: view thompson sampling in the GP setting.
References
[1] Williams “Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning” Machine Learning Vol. 8(3), pp. 229–256 1992
[2] Sutton & Barto “Reinforcement Learning: An Introduction” A Bradford Book 2018